XRD 분석, 그래프를 분석해보자! (2)

오늘은 XRD 그래프에서 peak가 일정한 폭을 가진채 나타나는 이유에 대해 알려드리겠습니다!

여러분은 sherrer equation에 대해 들어보신적이 있나요? sherrer equation은 XRD 그래프 분석을 통해 결정의 크기를 재는데 이용할 수 있는 관계식인데요, 바로 여기 그래프의 peak가 발생하는 이유와 엮어서 이해할 수 있습니다.

 

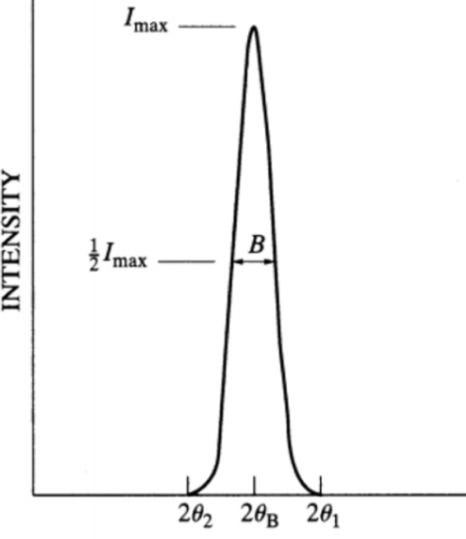
이상적인 상황(위), 실제 peak의 형태(아래)

이상적인 상황이라면, bragg의 법칙을 만족시키는 특정 각도에서만 peak가 발생해야하지만, 사실은 오른쪽의 그래프처럼 폭을 가진 형태로 나타납니다. 이때, 최대 intensity의 절반을 가지는 지점에서의 peak의 폭을 B: FWHM(Full width at half maximum) 또는 반치폭이라고 합니다. 이는,

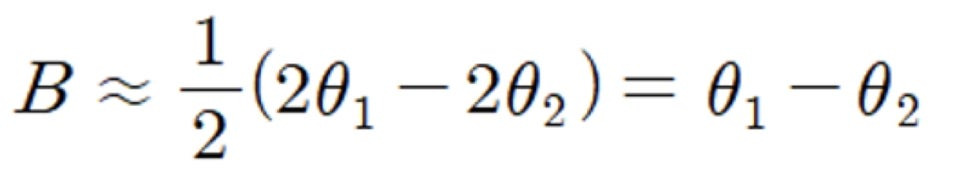
이런 식으로 나타낼 수 있고 근사치 값으로 나타냅니다. 일단 여기까지 반치폭에 대한 설명이었고, 다시 연관지어 설명 드릴테니까 기억하고 계셔야해요!

​

그렇다면, 저 폭이 소멸되는 경계조건은 과연 무엇이었을까요? 그것을 먼저 알아보도록할게요! 우선 각각 세타1과 세타2가 폭이 소멸되는 경계인데요.

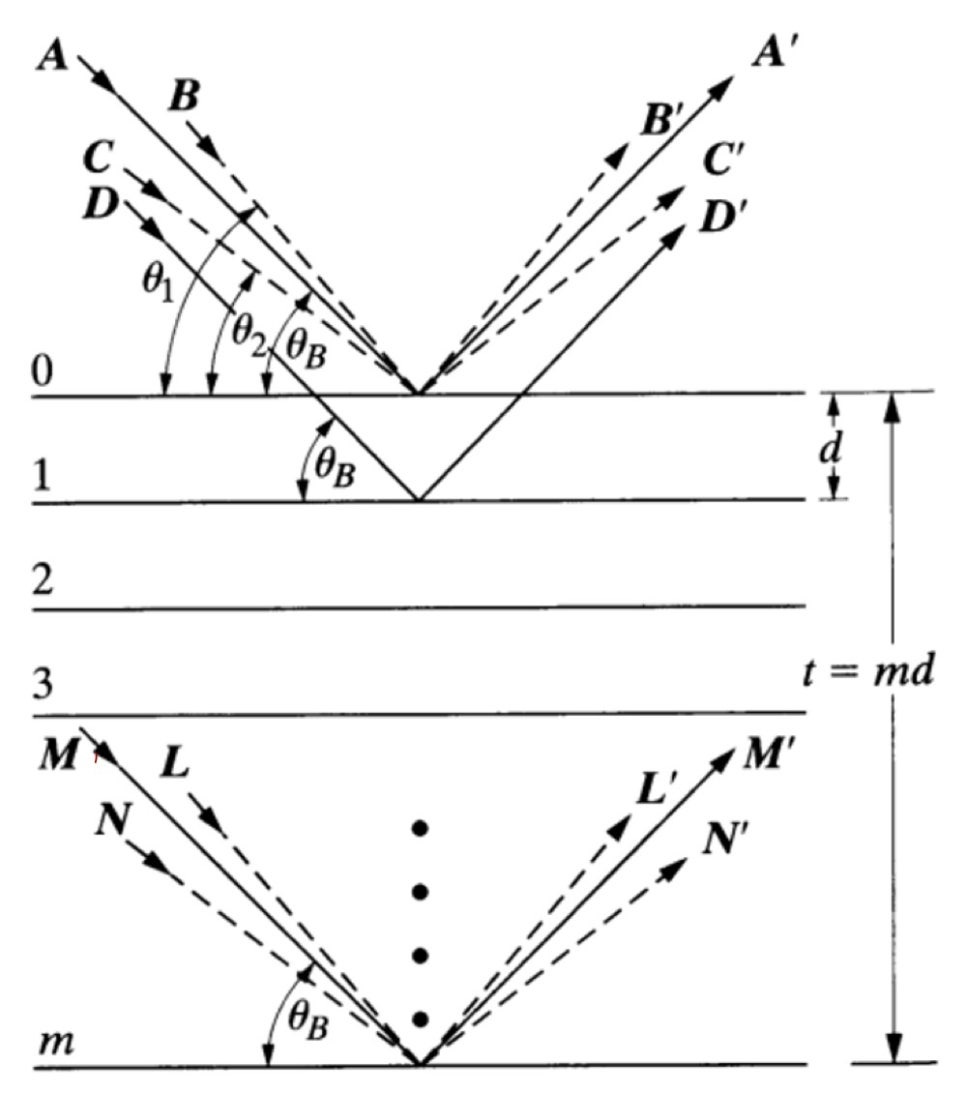
원래, 정상적으로 bragg의 법칙을 만족시키는 각도로 입사되는 빛을 A라고 할때, 더 큰 각도인 세타1으로 입사되어 상쇄간섭하는 B와 더 작은 각도인 세타2로 입사하여 소멸간섭하기 위한 및 C가 존재합니다.

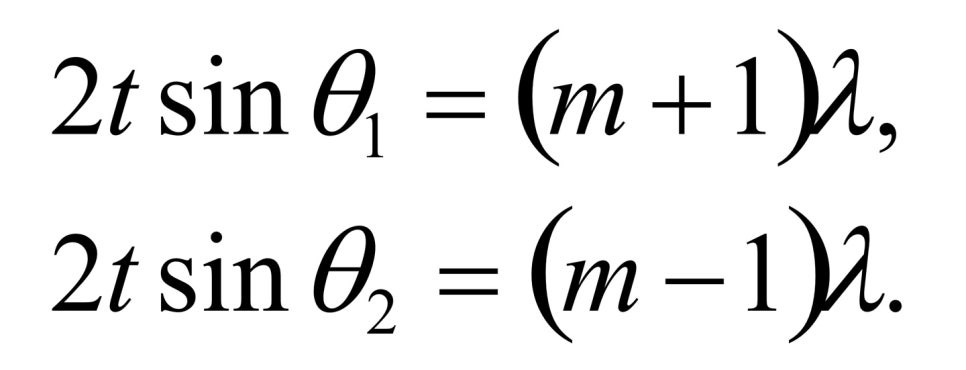
각 경계 조건을 이렇게 나타낼 수 있는데요. 우선 bragg의 법칙의 식을 그대로 인용했다고 할 수 있습니다. 먼저 t는 기존의 면간거리 t를 대체했죠. 이는 면간거리에 결정면간 거리의 개수를 곱한 값으로, 결정 전체의 길이입니다. 즉, 표면에서 산란되는 빛과 m번 째 면에서 산란되는 빛의 경로차를 의미합니다.

또한, m+1과 m-1의 조건은 1/2를 곱할 경우 중간 순서에 위치한 면과 표면의 경로차가 나오는데, 이는 m/2+1/2로, 경로차가 정수배가 아닌 반파장 만큼 더 난다는 것을 의미합니다. 즉, 표면에서 산란된 빛과 상쇄된다는 것을 의미합니다. 따라서, 면이 모두 짝을 이루어 모든 면에서 발생한 빛의 파장이 상쇄되어 결국 intensity가 나타나지 않는, peak폭이 사라지는 경계조건이 된다는 것을 의미합니다. m-1의 조건도 마찬가지의 매커니즘을 가집니다.

​

위의 식을 조합하면(뺀다면)

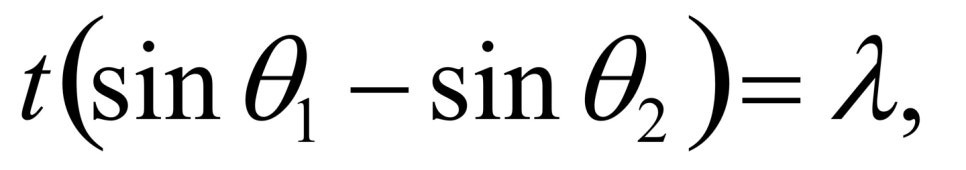
의 형태가 나오고 이것을 삼각함수 공식을 이용해 정리하면,

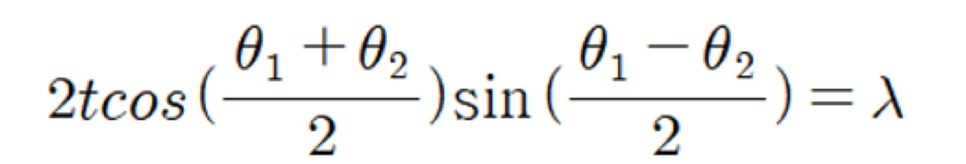
의 형태로 정리할 수 있습니다.

bragg angle이 세타1과 세타2의 중심에 위치해있으므로, 합이 거의 bragg angle의 두 배라고 할 수 있고,

(세타1 - 세타2)/2는 거의 0에 수렴하므로 위의 식처럼 sin값을 세타 1- 세타2로 근사할 수 있다.

다시 식을 정리해보면,

 

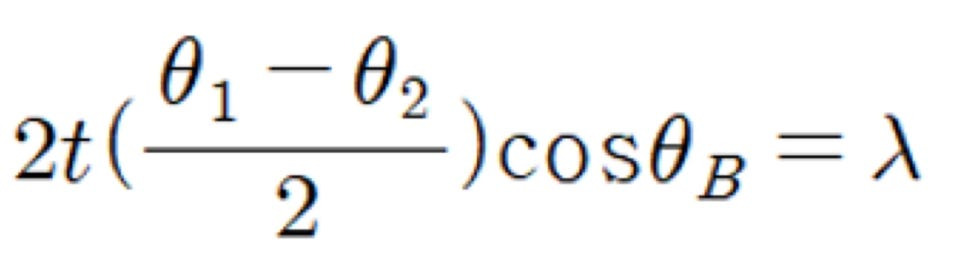
이렇게 표현됩니다. 어딘가 익숙한 것이 보이지 않나요?

앞서 말씀드린 반치폭이 보이는데요!

다음과 같이 반치폭을 나타낼 수 있다고 말씀을 드렸죠. 이 값을 대입을 하면!

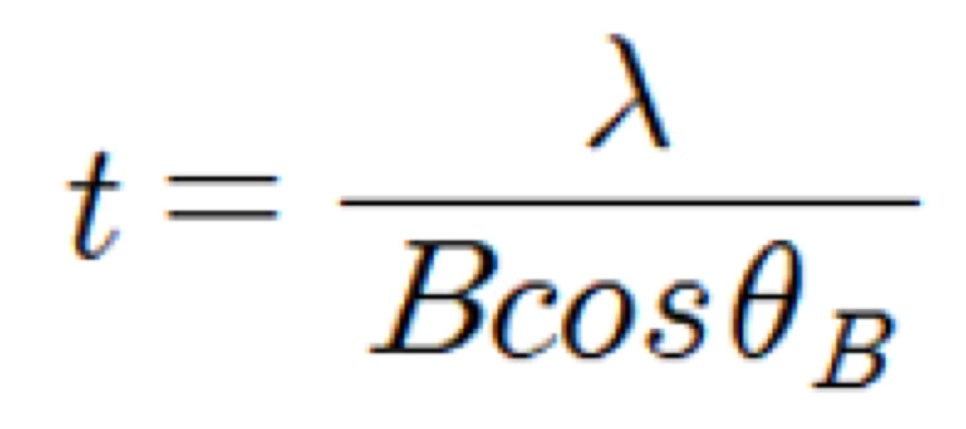
이렇게 최종적인 식을 나타낼 수 있습니다. 식을 해석하면, 결정의 두께 t는 반치폭을 이용하여 구할 수 있다는 것입니다! 수식적으로는 이러한데, 과연 실제 실험값도 일치할까요?

식의 형태가 거의 일치하죠! K는 결정마다 실질적인 모양이 다르기 때문에 모양을 보정해주기위해 보정상수로 들어갑니다. 하지만, 일반적으로 K는 0.9로 사용을 한다고하는데요, 즉, 수식적으로 구했을때와 동일하게, 반치폭을 이용하여 결정의 두께를 구할 수있다는 것입니다!

​

오늘은 이렇게, XRD 그래프의 peak가 폭을 가지는 이유와 결정 크기와의 관계에 대해 알아보았는데요. 유익하셨나요? 

다음에는 더 알찬 내용으로 돌아오도록 하겠습니다! 끝까지 읽어주셔서 감사합니다!